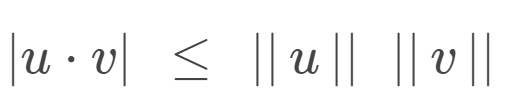A Beginner's Guide to Understanding Vectors for Linear Algebra
A fundamental concepts in data science and machine learning
Vectors
A vector is an ordered finite list of numbers. They are usually written as vertical arrays with squares.
They can also be written as numbers with commas and parentheses such as:
The elements of a vector are the values inside the array. The size is how many numbers of an element are contained. In this case, the vector above has four. A vector of size n is called an n-vector.
For two vectors that are equal (same size and each of the corresponding entries are the same), we will use an equal sign such as a = b. If they are n-vectors, then a = b means a_1 = b_1,…, a_n = b_n.
The values/numbers of elements in a vector are called scalars. If the scalars are real numbers, we have to refer to vectors as real vectors. This will cause the set of all values to be written as R, and n-vectors being R^n. So saying a ∈ R^n is like saying a is an element of R^n.
Block vectors
It’s sometimes beneficial to stack two or vectors such as
where a,b,c, and d are vectors.
Stacked vector a can be written as = (b,c,d). Stacked vectors can have scalars (numbers).
Subvectors
Let’s just pretend that b is an m-vector, c is an n-vector, and d is a p-vector. This would mean that b, c, and d are subvectors or slices of a, with m, n, and p, respectively.
Colon notation is used to denote subvectors. So if a is a vector, then a_r:s are:
The subscript r:s is called the index range.
Zero Vectors
A zero vector is where a vector with all elements equal to zero. The zero vector is denoted as 0, which is the same symbol used to denote the number 0. In computer programming, we call this overloading, which means that the symbol 0 has different meanings depending on the context.
Unit Vectors
A unit vector is where a vector with all elements equal to zero, but one of the elements equals one. Unit vectors are used to represent the axes of Cartesian coordinate systems. The standard unit vectors of the direction x, y, and z is:
Sparse
A vector is sparse whose entries contain many zeros, so like [1, 0, 0, 2, 0, 0, 0, 3, 0, 0, 0, 0, 4]. Unit vectors are sparse since most of their elements are zero, but just one element is non-zero. Zero vectors are the sparsest possible vector since all elements are zero.
Addition and Subtraction
Two vectors that are the same size can be added together. You would do so by adding the corresponding element. This would form another vector (same size) called the sum of the vectors. Addition in vectors used the plus symbol (+). For examples,
Subtraction is also the same. For example,
The outcome of vector subtraction is called the difference of two vectors.
Notes. Here are some things to keep in mind for any vectors of the same size:
Addition for vectors is commutative, so a + b = b + a
Addition for vectors is associative, so (a+b) + c = a + (b + c) can be written as a + b + c
Adding a zero vector to a vector doesn’t matter, so a + 0 = 0 + a = a
Substracting the same vector would give you the zero vector, so a - a = 0
Just a heads up that this would look different in programming languages. For example in computer programming (Python for example), [1, 5, 2] + [2, 3, 0] = [1, 5, 2, 2, 3, 0]. Programming languages put one vector after another. This is a valid expression in some programming languages, but it’s not the standard mathematical notation, which is what I’m using. Therefore it’s important to figure out if it’s a mathematical notation or the syntax of a programming language for manipulating vectors.
Scalar multiplication
Scalar multiplication is where the vector is multiplied by a scalar, which is done by multiplying every single element of the vector by the scalar. For example,
You can also put the scalar on the right. It will give you the same outcome,
Linear combination
You can achieve linear combinations by multiplying the vectors by the scalars and by adding them together. For example when using the axes of Cartesian coordinate systems,
Here is another perfect example when multiplying matrices,
Inner product
Inner product, also called dot product, is two vectors defined as the scalar, such as:
It is often denoted in angle brackets, but I’m not going to use it. An example of an inner product,
Notes. Pretty much the same as before. If a, b, and c are vectors that are the same size, and ω is a scalar (pretend it is), then:
There is commutativity such as a*b = b*a. The order doesn’t matter
There is associativity such as (ωa)*b = ω(a*b). We can rewrite it as ωa*b.
There is distributivity with addition such as (a+b)*c = a*c + b*c. The inner product can be distributed.
Norm
The Euclidean norm is the square root of the sum of the squares of its elements,
Sometimes the Euclidean norm is written with a subscript 2, such as ||x||_2. It indicates that entries of x are raised to the second power.
We can use norm for vectors such as,
Basically, if we use the norm equation with the elements in the vector, we’ll get this,
Similar to how the absolute value of a number measures its size, the norm of a vector measures its magnitude. If the norm of a vector is a small number, we describe the vector as small, and if the norm is a large number, we describe the vector as large.
Notes. Some important notes about the Euclidean norm:
Nonnegative homogeneity. ||βx|| = |β|||x||.
Triangle inequality. ||x+y|| ≤ ||x|| + ||y||.
Nonnegativity. ||x|| ≥ 0.
Definiteness. ||x|| = 0 only if x = 0.
A function that takes an n-vector and returns a real number, satisfying the four properties above, is known as a general norm.
Root-mean-square
Defined as:
Comparing the magnitudes of vectors with different dimensions can be challenging since the norms of these vectors may not be directly comparable. However, the root mean square (RMS) value of a vector provides a useful way to compare the norms of vectors with different dimensions.
Distance
The Euclidean distance is the length of the line between two vectors p and q:
The distance between two points with coordinates p and q can be calculated using the Euclidean distance formula, which is a standard way of measuring distance in one, two, and three dimensions.
When dealing with n-dimensional vectors, the RMS deviation between two vectors p and q is calculated by finding the RMS value of their difference, ||p-q||/sqrt{n}.
By calculating the RMS deviation between two n-vectors, we can obtain a quantitative measure of how different or similar the vectors are to each other.
The distance between two n-vectors can be used as a measure of their similarity. When the distance between two vectors is small, we describe them as close, which means that the vectors are similar in direction and magnitude. If the distance between two vectors is large, we describe them as far, indicating that the vectors are dissimilar in direction and magnitude.
Standard deviation
The standard deviation of a vector x provides information about how its individual entries deviate from their average value. A larger standard deviation indicates that the entries of the vector are more spread out and varied, whereas a smaller standard deviation suggests that the entries are more consistent and similar. When all entries of a vector are equal, the standard deviation of the vector is zero. In contrast, when the entries of the vector are almost the same, the standard deviation of the vector is small.
As an example, consider the vector x = (4,5,9,2,-3). Its mean is 3.4 and its standard deviation is 3.929 (population formula).
Some notes for standard deviation:
Adding a constant value to every entry of a vector does not affect its standard deviation.
Multiplying a vector by a scalar multiplies the standard deviation of the vector by the absolute value of the scalar. This means that if we multiply a vector by a scalar greater than one, its standard deviation will also increase proportionally. If we multiply the vector by a scalar between zero and one, its standard deviation will decrease proportionally.
Cauchy-Schwarz inequality
Cauchy-Schwarz inequality states that for any two vectors u and v in an inner product space, the absolute value of their dot product is less than or equal to the product of their norms:
Angle
The angle between two nonzero vectors is defined as:
This inequality can also be expressed in terms of the angle θ between vectors u and v as:
Clustering
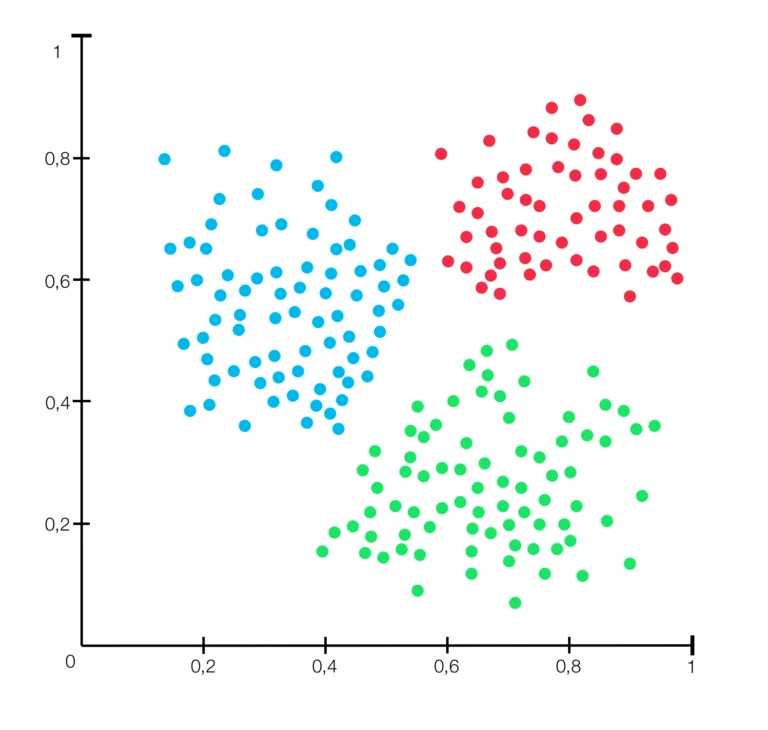
Clustering is a technique used in unsupervised learning that involves partitioning a set of vectors into k groups or clusters. The goal is to group vectors together that are similar to each other and dissimilar to vectors in other clusters. It is commonly used in image recognition and natural language processing. The whole point of clustering is to discover meaningful patterns and relationships among the vectors.
In the image above, the collection of vectors can be divided into k = 3 clusters, shown with colors representing different clusters. In many cases, it’s not like this image. Data is not as cleanly clustered.
K-means algorithm
The k-means algorithm is a popular clustering algorithm used in unsupervised learning. The k-means algorithm will try to find the local minimum of the within-cluster sum of squares (WCSS) objective function. It is often run multiple times with different initial centroids to increase the chances of finding a good clustering solution. You would then choose the one that has the smallest WCSS.
Will go more in-depth in a later article.
Linear Independence
A list of n-vectors is called linearly dependent if
holds for some a_1,…,a_k that are not all zero. Linear dependence is a property of a set of vectors where one or more of the vectors can be expressed as a linear combination of the other vectors in the set. This means that there are coefficients, not all zero, that can be multiplied by the vectors and added together to form a zero vector. The order in which the vectors are listed does not affect their linear dependence.
When a set of vectors is linearly dependent, there has to be at least one vector that can be expressed as a linear combination of the other vectors in the set.
Independent vectors
A list of n-vectors is called linearly independent if
only holds fr a_1 = 0. In other words, a set of vectors is linearly independent if the vectors that equal the zero vector are a linear combination with all coefficients equal to zero.
Notes.
A single vector is linearly dependent if it is the zero vector because any non-zero coefficient times the zero vector is also the zero vector. A single non-zero vector is always linearly independent because there are no other vectors for it to be dependent on.
[End]